Interesting article from Forbes ("Rotating Galaxies Could Prove Dark Matter Wrong") which includes the following graphic:
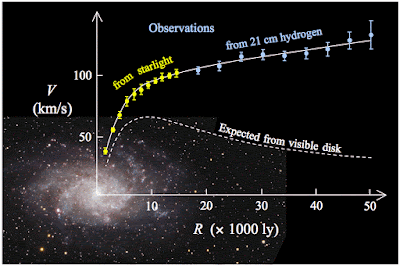
You can't argue with facts. The observed speeds are the observed speeds. The big mistake appears to be the other line for "Expected from visible disk".
What I don't get is why anybody would expect that in the first place. While the centres of galaxies are a lot denser than the outer bits, overall the matter is pretty evenly spread out (let's assume that the concentration of non-light emitting clouds of gas and dust are distributed in the same way as the visible stars).
Remember that a star at the outer edge of a galaxy only feels the pull of gravity inwards, but for a star further in, some of the inwards pull is cancelled out by the outwards pull of the stars further out.
Similarly, gravity from mass 'ahead' of the star, pulling it forwards is also cancelled out by gravity from mass 'behind' the star pulling it backwards. It is only the net inwards pull that matters.
In our Solar System, the Sun is 99.9% of the mass and thus causes 99.9% of the gravity and explains 99.9% of the orbits and speeds of the planets, but at a local level, the mass of a planet dictates the orbits of its moons. Earth is tiny compared to the sun, but a lot closer to the Moon. If you are calculating the orbit of the Moon, you first consider its orbit round Earth and then adjust that a bit for the influence of the Sun.
In the same way, the outer stars are orbiting round/in between/past each other as much as round the centre.
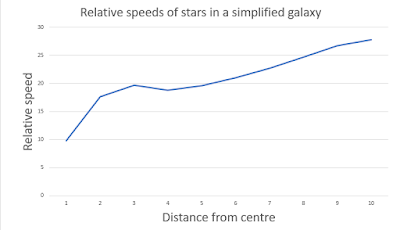
I did a spreadsheet for an idealised galaxy with
a) 11% of total matter in a circle with a radius of 2 "units" (multiples of 5,000 light years, let's say) from the centre and
b) the rest evenly spread out,
and calculated the relative net inward pull of gravity on a star orbiting 1, 2, 3 etc "units" from the centre.
The speed required to stay in a particular orbit is proportional to the force of gravity acting on it; there is no need to ponder whether a star's orbit dictates its speed; or whether its speed dictates its orbit; or a bit of both.
My spreadsheet produces a chart which shows that having made these assumptions, the relative force of gravity on a star travelling perpendicular to the centre at various distances along the radius matches up pretty well with the observations (the vertical axis units are not any absolute value, it's just relative to each other):
What we need is prevention
9 hours ago



16 comments:
I too looked into the subject of the gravity outside the radius of an orbit. The gravity of the mass outside the radius nets out and so leaving greater R greater mass inside R and greater velocity. It has been observed that the velocity carries on increasing in the outer area where mass drops off. Maybe the stars are younger and exhibit more mass at the outside , on the other hand they are very remote from the mass inside their orbits.
Din, that's along similar lines, but not the point I was trying to make.
For sure, greater R = greater mass inside R.
But it's not mass that matters so much as the total net inward gravitational force at any radius.
It's all about trade-offs and equilibrium.
In which case, greater R = more mass inside R, but you are further away from the bulk of the mass, so it largely cancels out. Hence flattish speeds as you go out.
I refer you to the illustrations at 4 and 5 of this post.
It's true that a star at 3 o'clock on an orbit is further away from the mass at 9 oclock but as the star orbits all of the mass inside providing the pull inwards and as the picture above shows there are less points of light outside of the central disc.
D, I don't think that galaxy is to scale.
My point is, the nearer a star is to the centre, the more mass there is outside it, pulling it outwards, cancelling out some of the mass pulling it inwards.
Merry Christmas!
It's documented in Newtowns law of gravity and the Shell theorum. There is no net pull outwards inside a sphere because the pull outwards is equal in all outward directions.
D, of course there is no net pull outwards. Where did I say that? Read what I explained.
The pull from gravity from mass outwards is equal in all outward directions, and so there is no outward pull that can be considered to be cancelling out any of the pull pulling inwards. That leaves the pull from the mass inwards pulling inwards.
Din, come off it.
It is widely accepted that the downwards pull of gravity of a planet is strongest exactly at sea level. If you go higher up, it is weaker (obviously).
If you dig down into the planet, there is more stuff above you, this pulls you up and there is less stuff beneath you pulling you down. The net downward pull is weaker.
Right at the centre, you don't feel any pull as all the mass around you is pulling you in equal and opposite directions.
See here.
Repeat on the scale of a galaxy, and..?
Its called Isaac Newton Law of Gravity Shell Theorem.
When thinking of digging down into the planet to a smaller radius and considering that there is is stuff above that radius pulling up, You are Forgetting to include all the mass on the opposite side of the sphere outside of the smaller radius, that is pulling down. And so that leaves only the gravitational pull of the smaller radius sphere. Its called Isaac Newton Law of Gravity Shell Theorem.
Isaac newtons law of gravity for spherical distribution of mass. The Gravitational pull at any point on a radius is the pull from inside the radius regardless of the mass outside of the radius as explained above. And so it as you go out the pull goes up.
In Summary
your post raised the issue in contemporary popular cosmology called the the galaxy rotation problem and considered the net gravitational forces of distributed rotating masses in a sphere. Isaac Newton provided the answer to net gravitational forces of masses distributed in a sphere. ie gravity pull on a point on a radius from masses outside of that radius and on opposite sides of the sphere including their distance from the point equal out , leaving only the pull from mass inside the radius. Spiral galaxy observations don't abide by it and that is what has led to what is called "the spiral galaxy rotation problem." that your post was referring to.
Din: "You are Forgetting to include all the mass on the opposite side of the sphere outside of the smaller radius, that is pulling down."
That is exactly what I am not doing!! I refer you to the illustrations yet again. I clearly show the bits whose net effect is zero and which bits are left over.
I've genned up again on Newton's Shell Theorem, it predicts the same results as I do and is based on same assumptions and reasoning. It is just that he was a maths genius without a computer who had to invent calculus instead, which gave him the shortcut that you can ignore outer shells.
I am a good at maths and armed with a computer so I can calculate it the hard way very easily without ignoring anything at all.
They both come to pretty much the same result, of course.
Din, last two comments, agreed (finally).
That works for spherical distribution of mass (where mass inside radius is a cubic function) but galaxies are effectively discs (or very flat cylinders) and so mass inside a radius is a square function, gravity is an inverse square function and the two exactly cancel out.
Applying Newton's logic to gravity inside a flat and uniform disc, it is exactly the same wherever you are (except dead centre).
Which neatly explains why rotation speed is pretty flat all the way out!!
Another curious observation which is very difficult to explain is that all disc galaxies appear to take roughly a billion years to rotate once, no matter what their radius, how many stars they contain, or how those stars are distributed within the galaxy. See the article on astronomy.com
Even if you invoke dark matter you have to explain why it just so happens that each disc galaxy has exactly the right amount of dark matter to make this happen. And without dark matter Newtonian/Einsteinian gravity just doesn't explain it at all.
Very strange!
D, I hadn't read that before - fascinating!
Newton/Einstein gravity explain everything perfectly (give or take a bit of MOND), I don't know why anybody would think otherwise. The whole 'dark matter' theory is a load of bollocks dreamed up by physicists looking for grant money to fund ever more expensive projects, knowing perfectly well they'll never find it.
It's like getting a full time job looking for the Loch Ness monster - you'll never find it, so you're job is permanent, but you have to keep flagging up possible sightings that can only be verified by having more researchers and more equipment.
Post a Comment