See e.g. The Daily Express.
1. Here's the basic question. Let's assume side length is 10, for sake of argument.
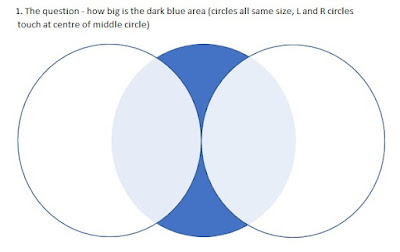2. Draw the overlapping bits (dotted outlines) and an isosceles triangle (red outlined),
3. Work out area of the sector (pink). If you can't guess that this is one-third of the area of a circle (which seems a bit obvious, with the benefit of hindsight), you need to work out the angle of the right-hand corner of the triangle (which touches the circle in the centre).
From 3. below, it is 120 deg, which is a third of a full circle 360 deg, so the pink sector has area = pi x r^2 ÷ 3 = 100/3 pi (about 105, in old money).
4. Focus on the triangle (from 2. above).
Sides are all the same length r = 10, so it is an isosceles triangle and angles = 60 deg.
Angle of the triangle on the right where it touches the centre of the circle = 120 deg. (needed for 3. above).
Fold it in half (middle triangle) and the bottom side is half r = 5.
The vertical side is the square root of r^2 - 1/2 r^2 = square root of 3/4 r^2 = square root of 75.
The area of the triangle on the right (or on the left, for that matter) = base x height x 1/2
= 5 x square root of 75 = about 43 in old money.
5. Subtract this from the area of the sector. The pink segment left over thus has area = (100/3 pi) - (5 x square root of 75)
= about 62 in old money.
6. Then subtract four of these segments from the area of a full circle = 100 pi - 4 x ((100/3 pi) - (5 x square root of 75))
= 100 pi - 400/3 pi + 20 x square root of 75
= - 100/3 x pi + 20 x square root of 75
which simplifies slightly to:
= - 100/3 x pi + 10 x square root of 300.
= which is about 68.5 in old money.
Looks about right, that's a bit more than one-fifth of the area of the circle (which is about 314).
If you want to boil it down to an equation for the blue area, I think it is:
= -(pi x r^2)/3 + (r x sq root of (3 x r^2)),
UPDATE - Bayard in the comments and Nigel S. via email point out that this can be expressed more elegantly as:
r^2 x (-pi/3 + sqrt(3))
Sunday, 22 May 2022
'Impossible' GSCE Maths question?
Subscribe to:
Post Comments (Atom)
12 comments:
Like so much of the maths curriculum, this could be vital if you had ambitions to be a circlologist: otherwise totally useless.
DCB, yes of course.
"2. Draw the overlapping bits (dotted outlines) and an isosceles triangle (red outlined),"
It's very much simpler when you realise that the triangle has to be an equilateral triangle from the get-go.
Working: the pale blue areas have to be symmetrical about a line drawn from one vertex to the other because all the circles are the same size.
Therefore the right hand side of the red triangle has to be the same as the left hand side. We know that the RHS and the base are radii of the circle, therefore the triangle is equilateral and the angles are all 60 degrees.
From this we can deduce that the two lines from the centre of the RH circle to the vertices of the pale blue area are at an angle of 120 deg to each other, therefore the pink area is one third of the circle.
The equilateral triangle has area half base times height, therefore two of the triangles will be base (= radius = r) x height. Height(as you point out) = root (r^2 - (r/2)^2) = r x root(3/4)= r x root3/2
Thus area of two triangles = r^2 x root3/2
The area of the circle is pi x r2, therefor the area of a third of it is pi x r^2/3,
therefore the area of the area of the light blue area in fig 1 is 2/3 of a circle plus (two thirds of a circle minus four triangles)
= 4/3 circle minus two times r^2 x root3/2
= 4/3 pi r^2 - root3/2 r2
= r^2 (4/3 pi -root3/2)
and so the dark blue area is pi r^2 - r^2 (4/3 pi -root3/2)
= r^2 (pi-(4/3 pi -root3/2))
= r^2 (root3/2) -(1/3 pi)
I think.
B "2/3 of a circle plus (two thirds of a circle minus four triangles)"
I don't think so. I think it is.
"one circle MINUS (four x (third of a circle minus a triangle))"
open brackets
"negative one-third of a circle PLUS four triangles"
= - 105 + (4 x 43) = 67 area
Can you put hard numbers in and expand your brackets?
Hard numbers, if radius = 10.
Full circle area = 314
Triangle area = 43.
Nope,
Fig 3 pink area is 1/3 of the circle.
Fig 4, third diagram, reflect that in its vertical axis. You now have half of the Fig 1 light blue area. You can see that within that half light blue area fit two of the equilateral triangles, also that the Fig 3 pink area is equal to half the light blue area if you subtract two of the small crescents that surround the two equilateral triangles and also that if you subtract two of the small crescents from the pink area, you are left with the two equilateral triangles. So the light blue area = 2 times (1/3 of a circle + 2 crescents) = 2/3 circle + 4 crescents.
1/3 circle - two equilateral triangles = 2 crescents, therefore 2/3 circle - four equilateral triangles = 4 crescents.
So the light blue area = 2/3 circle + 2/3 circle - four equilateral triangles = 4/3 circle - four equilateral triangles.
Therefore the dark blue area = 1 circle - 4/3 circle plus four equilateral triangles = four equilateral triangles - 1/3 circle
I have just realised there is a much simpler way of doing this:
From Fig 2 it is obvious that the dark blue area is one of the equilateral triangles + a crescent (on top)- 2 crescents (either side),
so both dark blue areas = two triangles - 2 crescents.
1/3 circle - two equilateral triangles = 2 crescents (from above)
therefore both dark blue areas = two triangles - 1/3 circle + two equilateral triangles = four equilateral triangles - 1/3 circle
It's always best to try and stay away from putting values in, otherwise you may end up with a solution that only works for your chosen values and no other.
Disclaimer: I did do Maths A level and went on to read Engineering, however, the reasoning doesn't seem to require more than a knowledge of Pythagoras's theorem and the formula for the area of a circle, both of which I had learned before I was 13.
B "it's always best to try and stay away from putting values in, otherwise you may end up with a solution that only works for your chosen values and no other."
Sure. Which is why I road test these using different radii, algebra, grind, common sense, guesswork until I get a universal solution.
"Sure. Which is why I road test these using different radii, algebra, grind, common sense, guesswork until I get a universal solution."
The whole point of using variables is to remove the necessity to do all that. If it works with the variables, it is the universal solution.
B, sure, but your answer is clearly wrong and mine is in fact correct.
OK, if the radius is 10, then the area of one equilateral triangle = 43.3, we agree on that.
Therefore the area of four equilateral triangles is 173
The area of a third of a circle is 314/3 = 104
Therefore the dark blue area = 69
How is that wrong when you got 68.5?
Area of triangle = ((root3)/2) x r x r/2 = r^2(root3)/4
Four triangles = root3 x r^2
One third of a circle = pi r^2/3
Therefore blue area = r^2(root3-(pi/3)) = 68.5 r^2
B, yup, I couldn't follow your explanation
68.5 is correct.
"r^2(root3-(pi/3))" is also correct.
That's the same as my
-(pi x r^2)/3 + (r x sq root of (3 x r^2))
Only expressed more elegantly, as somebody already pointed out to me in an email.
I rather gave up on that explanation when I realised there was a simpler way.
Post a Comment