A regular polygon with two and a half sides

You calculate the interior angle in degrees using the formula ((N-2) x 180)/N.

For a four sided regular polygon (spoiler alert: a square) has an interior angle in degrees of ((4-2) x 180)/4 = 90. So you draw a four sided regular polygon by going a certain distance, turning right to make a corner with a 90 deg interior angle and going the same distance again, repeat until you get back to the starting point X:



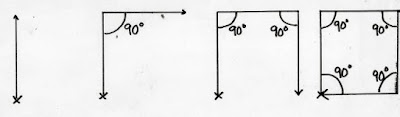
That's easy enough, you can do the same for three sides, or five or six or anything until you approach a circle.

But this is maths and N can be any number you like. So let's try two and a half sides.

Interior angle in degrees = ((2.5 - 2) x 180)/2.5 = 36

Let's repeat the process, draw a line, turn right so the interior angle is 36 degrees and draw another line, then keep going until you get back to your starting point:



That is not a 'pentagram', it is a regular polygon with two and a half sides.

It is important to note that the edges do not actually touch each other where they appear to cross, those are not real corners, it just seems that way if you reduce this shape to a two-dimensional representation.
-----------------------------------------
There is a formula for calculating the number of diagonals, which is (N x (N-3))/2.

So a square has (4 x (4-3))/2 = 2 diagonals.

And a two and a half sided one should have (2.5 x (2.5-3))/2 = negative 0.625 diagonals i.e. none.
------------------------------------------
Calculating the surface area is a bit trickier, see part 2.
-----------------------------------------
You can also have a regular polygon with three-quarters of a side.

Interior angle in degrees = ((0.75 - 2) x 180)/0.75 = 300. What you end up with looks like an equilateral triangle, but the area of the polygon is everything outside the triangle, not inside it.

(You get a similar looking result if you try N = -3, an equilateral triangle in the middle that is outside the shape, and everything outside it is the polygon, but the surface area is the negative of the area outside. Can things have a negative area? Probably not, but no more than they can have a negative number of sides.)

Sadly, this doesn't work very well with other fractions, if N is 1/3 or 1/2, the interior angle is a multiple of 180 degrees, so it is just a straight line going there and back.

If N is 2/3, the interior angle is 360 degrees, so it's just a straight line going on forever and you never get back to the starting point.